Prionic epigenetic memory

Here I'll describe a toy model of a molecule that catalyzes its own creation—providing a very simple form of epigenetic memory. Though loosely inspired by prion-based memory in yeast, in fact the model illustrates principles common to other epigenetic systems, such as those involving the spreading of histone modifications.

Let's suppose that there are two types of molecules, X and Y, subject to two basic reactions:

1. Creation of X molecules at a constant rate $k$
2. Conversion of X to Y molecules, catalyzed by existing Y molecules, with rate constant $s$

In the "prion" interpretation, Y is like a misfolded, prion form of a protein X. But this could also be a toy model for the spreading of a histone mark in a genomic region—viewing X as an unmarked histone and Y as a marked one, with the conversion reaction representing the "spreading" of the mark mediated by a reader-writer enzyme.

We'll suppose these reactions occur in dividing cells, with molecules randomly assorted to daughter cells at division (at times T = 1, 2, 3, ...). On average this will halve molecule counts every generation. Overcoming this dilution—an inevitable consequence of cell growth and division—is the fundamental challenge for memory maintenance.

Stochastic simulation

To capture the inherently stochastic nature of reactions at the molecular scale, let's implement an exact stochastic simulation of this system using Gillespie's algorithm (written in Mathematica):

GillespieStep[{x_, y_, t_}, k_, s_] :=
    Flatten[{{x, y} + RandomChoice[{k, s x y} -> {{1, 0}, {-1, 1}}],
        t + RandomVariate[ExponentialDistribution[k + s x y]]}];

This function implements a single step of the algorithm, taking the current state of the system, selecting a reaction to occur (either creation of X or conversion of X to Y), and then returning the new system state and time.

The following function simulates dynamics until a fixed time T = 1, representing one cell cycle:

PrionDynamics[{x_, y_}, k_, s_] :=
Take[NestWhileList[
    GillespieStep[#, k, s] &, {x, y, 0}, (#[[3]] < 1) &][[-2]], {1, 2}];

To model cell division, we randomly partition molecules to daughter cells, which amounts to drawing from a binomial distribution:

Assort[{x_, y_}] := {RandomVariate[BinomialDistribution[x, 1/2]],
        RandomVariate[BinomialDistribution[y, 1/2]]}

We are going to follow just one cell lineage through successive divisions—this represents tracking a single branch of the cellular genealogy, as one would observe if following a single cell in a growing colony.

Putting everything together, we can simulate many generations of growth and division, and plot the number of X and Y molecules over time:

ListLinePlot[
        Transpose@
            NestList[Assort[PrionDynamics[#, 18.0, 0.1]] &, {10, 10}, 2000],
        Frame -> True, LabelStyle -> {Black, 18},
        FrameLabel -> {"Time (cell generations)", "Molecule count"},
        PlotLegends -> {"X", "Y"}]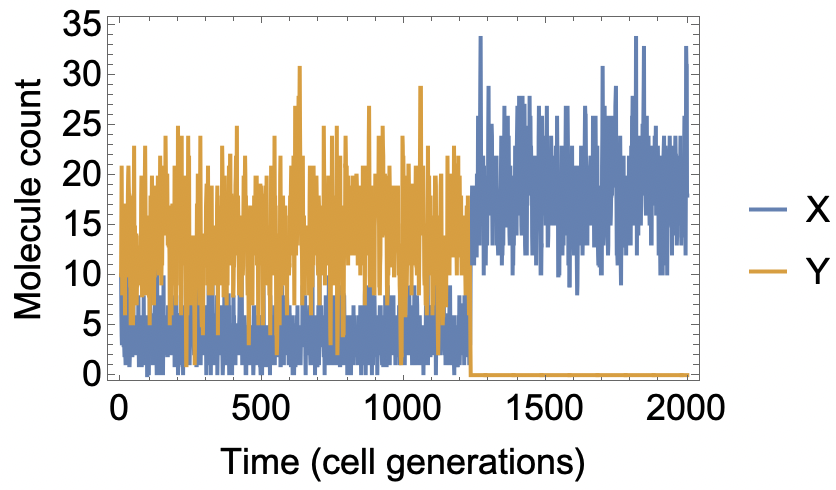

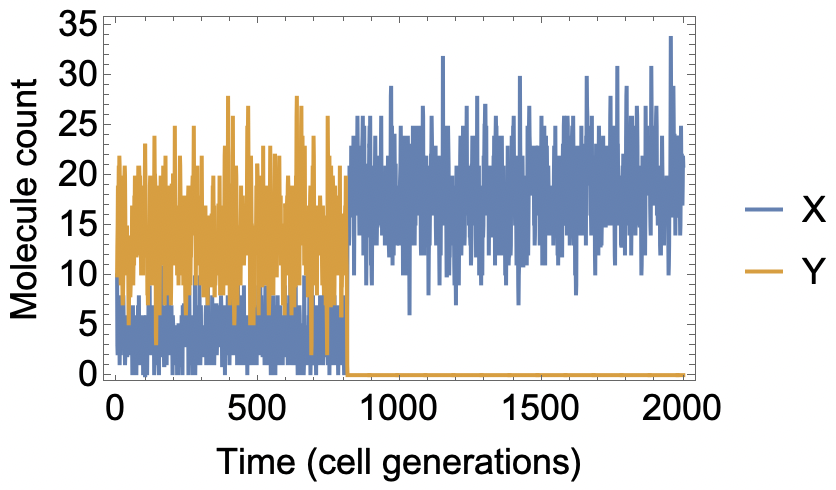
For these parameter choices, we get around 20 molecules total (X and Y). If we start with at least some Y molecules, on average the system will remain in a "Y rich" state for a long time (~1000 generations), even though the alternative "Y free" state is completely stable. This is the epigenetic memory in the model. The memory is lost when, by chance, all the Y molecules are lost at once (e.g. assorting all to one daughter cell in a cell division).

Exponential scaling of memory stability

So 20 molecules can give us at least ~1000 generations of memory. Is this the best we can do with 20 molecules? And what if we have more molecules?

The best case for the memory turns out to be when $s$ is very large, so that if any Y is present, X molecules instantly become Y when they are created. In this case, we can just keep track of how many Y molecules there are. They are effectively created at rate k, and are periodically diluted by cell division. We start with some number, and at some point, stochastically, they will all be lost. This is when the memory is lost.

Intuitively, it seems as though the time until this loss event should scale exponentially with the typical number of molecules $N$ in the system, because it requires all Y molecules to be lost at once at a cell division, which happens with probability $2^{-N}$. In fact, this is not quite right, because the number of molecules fluctuates. However, numerically simulating the system for different values of $k$ and comparing the average number of molecules to the lifetime, we find our intuition is qualitatively correct—there is an exponential scaling of memory stability:

dat = Table[{1.5 k, 
    Around@Table[
      Length[NestWhileList[
        RandomVariate[
          BinomialDistribution[# + 
            RandomVariate[PoissonDistribution[k]], 1/2]] &, 
        Ceiling[k] , (# > 0) &, 1, 10000]], {1000}]}, {k, 0.5, 6, 
    0.5}];
Show[ListLogPlot[{#[[1]], #[[2, 1]]} & /@ dat, PlotStyle -> Black], 
 Frame -> True, 
 FrameLabel -> {"Mean number of molecules", 
   "Memory stability (generations)"}, LabelStyle -> {Black, 18}]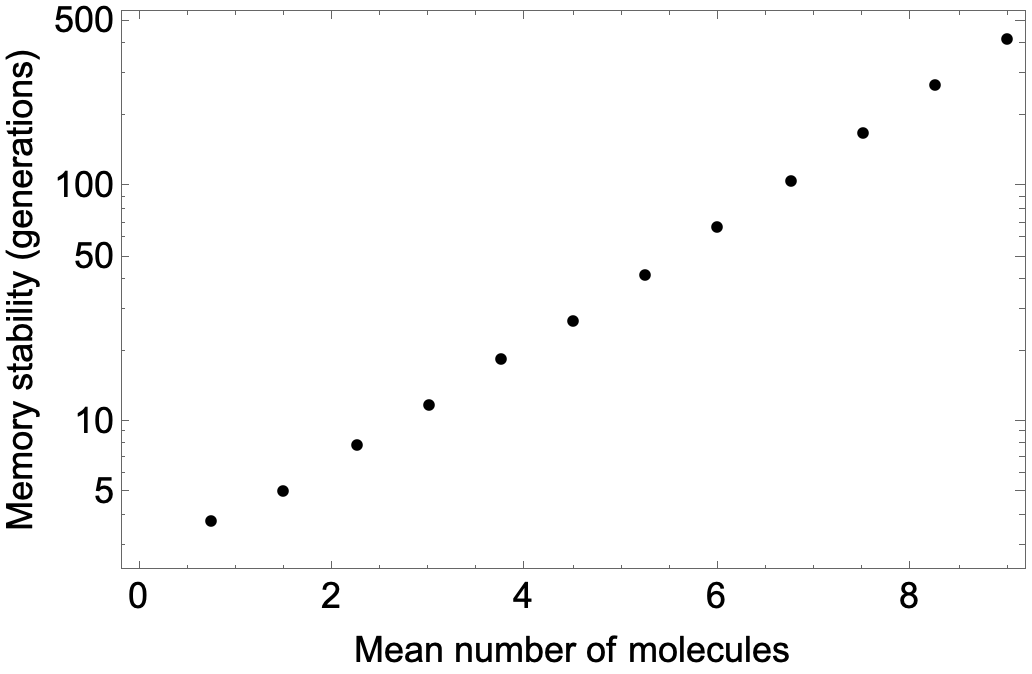

This exponential scaling of stability with system size is typical of bistable switches, such as the genetic toggle switch. I suspect exponential scaling in $N$ arises generally in chemical reaction networks whenever the deterministic (large $N$) limit is multistable. Interestingly, Biancalani and Assaf (2015) show that a toggle switch lacking cooperativity, whose deterministic limit is not bistable, exhibits instead a merely quadratic scaling of lifetime with system size.

Postscript

An interesting subtlety here which I didn't notice initially: the volume of growing cells increases over the course of the single cell cycle, which means that the bimolecular conversion reaction of X to Y must slow down over the course of the cell cycle! Though getting this right shouldn't matter for our qualitative story here, it is interesting because it is not completely obvious how to do exact stochastic simulation with this kind of time-dependent rate. A solution can be found in this 2004 paper from Ting Lu, Jeff Hasty, and others.